imgsthumb_37.jpg

冒泡排序、插入排序、希尔排序、归并排序、快速排序和堆排序，是常用的几种排序方法，特别是冒泡、快速排序，也是应用比较广泛的算法之一，本文部分内容整理自网络，代码均已使用C++和C语言实现。

概述

排序方法 平均情况 最好情况 最坏情况 空间复杂度 稳定性
冒泡排序 $O(n^2)$ $O(n)$ $O(n^2)$ $O(1)$ 稳定
插入排序 $O(n^2)$ $O(n)$ $O(n^2)$ $O(1)$ 稳定
希尔排序 $O(n^{1.3})$ $O(nlogn)$ $O(n^2)$ $O(1)$ 不稳定
快速排序 $O(nlogn)$ $O(nlogn)$ $O(n^2)$ $O(nlogn)$ 不稳定
归并排序 $O(nlogn)$ $O(nlogn)$ $O(nlogn)$ $O(n)$ 稳定
堆排序 $O(nlogn)$ $O(nlogn)$ $O(nlogn)$ $O(1)$ 不稳定

冒泡排序

冒泡排序（bubblesort）是先从数组第一个元素开始，依次比较相邻两个数，若前者比后者大，就将两者交换位置，然后处理下一对，依此类推，不断扫描数组，直到完成排序。时间复杂度最好为$O(n)$，最坏为$O(n^2)$，平均为$O(n^2)$。空间复杂度为O(1)。它是稳定的排序算法。

示意图

maopao1.gif

C++实现

void bubbleSort(vector<Comparable> & a) {
        int len = a.size();
        for(int i=0; i<len-1; i++)  {
            for(int j=0; j<len-1-i; j++) {
                if(a[j] > a[j+1]) {
                    swap(a[j], a[j+1]);
                }
            }
        }
    }

C语言实现

void BubbleSort(int arr[], int length)
    {
        int i = 0;
        int j = 0;

        if(length < 1)
        {
            return;
        }


        for(i = 0; i < length - 1; i++)
        {
            for(j = i + 1; j < length; j++)
            {
                if(arr[i] > arr[j]){
                    swap(&arr[i], &arr[j]);
                }    
            }
         }
    }

插入排序

插入排序（insertsort）是逐一取出元素，在已经排序的元素序列中从后向前扫描，放到适当的位置，它保证了从位置0到位置i-1上的元素是已经排序好的。时间复杂度最好为$O(n)$，最坏为$O(n^2)$，平均为$O(n^2)$。空间复杂度为$O(1)$。它是稳定的排序算法。

示意图

charu2.gif

C++实现

void insertSort(vector<Comparable> & a) {
        int len = a.size(), j;
        for(int i=1; i<len; i++) {
            Comparable tmp = a[i];
            for(j=i; j>0 && tmp<a[j-1]; j--){
                a[j] = a[j-1];
            }
            a[j] = tmp;
        }
    }

C语言实现

void InsertSort(int arr[], int length)
    {
        int i = 0;
        int j = 0;
        int tmp = 0;

        if(length < 1)
        {
            return;
        }
        for(i = 1; i < length; i++)
        {
            tmp = arr[i];
            for(j = i; j > 0 && arr[j - 1] > tmp; j--)
            {
                arr[j] = arr[j - 1];
            }
            arr[j] = tmp; 
        }
    }

希尔排序

希尔排序（shellsort），也称缩小增量排序，实质是分组插入排序,选择一个步长，然后按间隔为步长的单元进行排序，步长递归变小，直至为1。时间复杂度最好为$O(nlogn)$，最坏为$O(n^2)$，平均为$O(n^{1.3})$。空间复杂度为O(1)。它是不稳定的排序算法。

原数组：[13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10]
我们以步长为5开始进行排序(一般初始步长为数组长度的一半)，先分组：
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
分组后进行排序：
[10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45]
然后再以3为步长进行排序，先分组：
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45
分组后进行排序：
[10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94]
最后以1步长进行排序（此时就是简单的插入排序了）。

示意图

xier3.gif

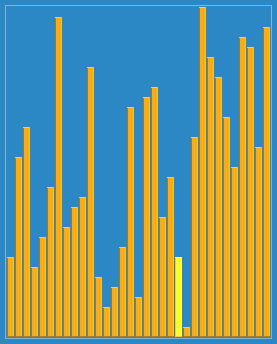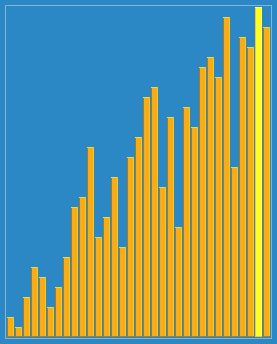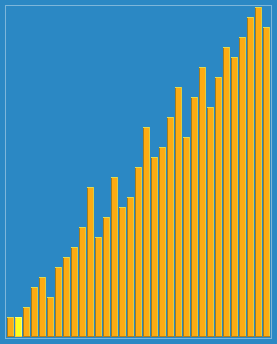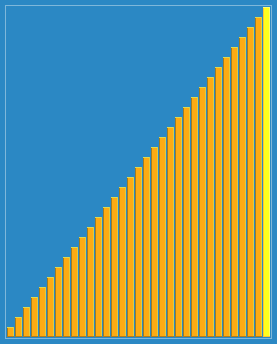
C++实现

void shellSort(vector<Comparable> & a) {
        int len = a.size(), j;
        for(int gap=len/2; gap>0; gap/=2) {
            for(int i=gap; i<len; i++) {
                Comparable tmp = a[i];
                for(j=i; j >= gap && tmp<a[j-gap]; j-=gap) {
                    a[j] = a[j-gap];
                }
                a[j] = tmp;
            }
        }
    }

C语言实现

void ShellSort(int arr[], int length)
    {
        int i = 0;
        int j = 0;
        int duration = 0;
        int tmp = 0;

        if(length < 1)
        {
            return;
        }

        for(duration = length / 2; duration > 0; duration /= 2)
        {
            for(i = duration; i < length; i++)
            {
                tmp = arr[i];
                for(j = i; j >= duration; j -= duration)
                {
                    if(tmp < arr[j - duration])
                    {
                        arr[j] = arr[j - duration];    
                    }
                    else
                    {
                        break;
                    }
                }
                arr[j] = tmp;            
            } 
        } 
    }

快速排序

快速排序（quicksort），先选择枢纽元，然后把比它小的放在左边，大的放在右边，然后再对左右区间分别使用这一过程，直到区间内只剩一个元素。时间复杂度最好为$O(nlogn)$，最坏为$O(n^2)$，平均为$O(nlogn)$。空间复杂度为$O(nlogn)$。它是不稳定的排序算法。枢纽元的选取使用三数中值法。

示意图

kuaisu4.gif

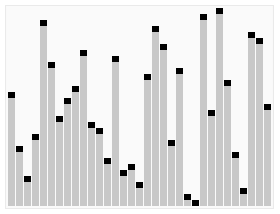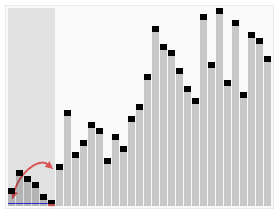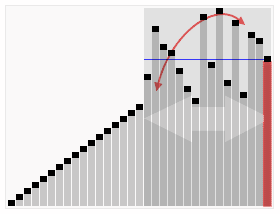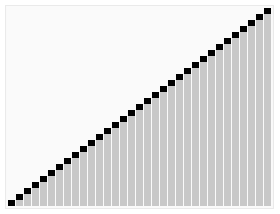
C++实现

//使用三数中值法取枢纽元
template <typename Comparable>    
const Comparable & median3(vector<Comparable> & a, int left, int right) {
        int center = (left + right) / 2 ;
        if(a[center] < a[left]) {
            swap(a[left], a[right]) ;
        }
        if(a[right] < a[left]) {
            swap(a[left], a[right]);
        } 
        if(a[right] < a[center]) {
            swap(a[center], a[right]);
        }
        return a[center];    //在返回中值的时候已经对首、中、尾三个元素进行了排序 
    }

    template <typename Comparable>
    void quicksort_l(vector<Comparable> & a, int left, int right) {
        Comparable pivot = median3(a, left, right);
        int i = left, j = right;
        do {
            while(a[++i] < pivot) {    }    //首、中、尾三个元素已经进行了排序 
            while(pivot < a[--j]) {    }
            if(i < j) {
                swap(a[i], a[j]);
            }         
        } while(i<=j);
        if(left < j) quicksort_l(a, left, j);     //对左区间内的元素排序 
        if(i < right) quicksort_l(a, i, right);    //对右区间内的元素排序     
    }

    template <typename Comparable>
    void quickSort(vector<Comparable> & a) {
        quicksort_l(a, 0, a.size() - 1);
    }

C语言实现

void Qsort(int arr[], int start, int end)
    {
        int lt = start;
        int gt = end;
        int i = start + 1;
        int pivot = arr[start];

        if(start >= end)
        {
            return;
        }

        while(i <= gt)
        {
            if(arr[i] < pivot)
            {
                swap(&arr[lt++], &arr[i++]);
            }
            else if(arr[i] > pivot)
            {
                swap(&arr[gt--], &arr[i]);    //此处不能i++，否则原来gt指向的元素没有与pivot进行比较
            }
            else
            {
                i++;
            }        
        }

        Qsort(arr, start, lt - 1);
        Qsort(arr, gt + 1, end);
    }

    void QuickSort(int arr[], int length)
    {
        if(length <= 0) 
        {
            return;
        }

        Qsort(arr, 0, length - 1);
    }

## 归并排序

归并排序（mergesort）是将数组分成两半，这两半分别排序后，再归并在一起。排序某一半时，继续沿用同样的排序算法，最终你将归并两个只含一个元素的数组，这样算法的重担都落在“归并”的部分上。该算法是采用分治法的一个非常典型的应用。时间复杂度都为$O(nlogn)$。空间复杂度为$O(n)$。它是稳定的排序算法。

示意图

binggui5.gif

C++实现

template <typename Comparable>
void merge(vector<Comparable> & a, vector<Comparable> & tmpArray, int leftPos,  
int rightPos, int rightEnd) {
    int leftEnd = rightPos - 1;        //center
    int tmpPos = leftPos;
    int numElements = rightEnd - leftPos + 1;
    while(leftPos <= leftEnd && rightPos <= rightEnd)  {
        if(a[leftPos] <= a[rightPos]) {
            tmpArray[tmpPos++] = a[leftPos++];
        } else {
            tmpArray[tmpPos++] = a[rightPos++];
        }
    }
    while(leftPos <= leftEnd) {        
        tmpArray[tmpPos++] = a[leftPos++];
    }
    while(rightPos <= rightEnd) {
        tmpArray[tmpPos++] = a[rightPos++];
    }
    for(int i=0; i<numElements; i++, rightEnd--) {
        a[rightEnd] = tmpArray[rightEnd];
    }
}

template <typename Comparable>
void mergeSort_l(vector<Comparable> & a, vector<Comparable> & tmpArray, int left, int right) {
    if(left < right) {
        int center = (left + right) / 2;
        mergeSort_l(a, tmpArray, left, center);        //对半个数组分别进行排序 
        mergeSort_l(a, tmpArray, center+1, right);
        merge(a, tmpArray, left, center+1, right);
    }
}

template <typename Comparable>
void mergeSort(vector<Comparable> & a) {
    vector<Comparable> tmpArray(a.size());
    mergeSort_l(a, tmpArray, 0, a.size()-1);
}

C语言实现

void Merge(int arr[], int tmpArr[], int leftPos, int rightPos, int rightEnd) 
{
    int i = leftPos;
    int j = rightPos;
    int tmpPos = 0;
    int numElements = rightEnd - leftPos + 1;
    int leftEnd = rightPos - 1;

    for(tmpPos = leftPos; tmpPos <= rightEnd; tmpPos++)
    {
        if(i > leftEnd)
        {
            tmpArr[tmpPos] = arr[j++];
        } 
        else if(j > rightEnd)
        {
            tmpArr[tmpPos] = arr[i++];
        }
        else if(arr[i] <= arr[j])
        {
            tmpArr[tmpPos] = arr[i++];
        }
        else
        {
            tmpArr[tmpPos] = arr[j++];
        }
     }

     for(i = 0; i < numElements; i++, rightEnd--)
     {
         arr[rightEnd] = tmpArr[rightEnd];
     }
}

void MSort(int arr[], int tmpArr[], int start, int end)
{
    int mid = 0;

    if(start >= end)
    {
        return;
    }

    mid = (start + end) / 2;
    MSort(arr, tmpArr, start, mid);
    MSort(arr, tmpArr, mid + 1, end);
    Merge(arr, tmpArr, start, mid + 1, end);
}

void MergeSort(int arr[], int length)
{
    int *tmpArr;

    tmpArr = (int *)malloc(length * sizeof(int));
    if(tmpArr != NULL) 
    {
        MSort(arr, tmpArr, 0, length - 1);
        free(tmpArr);
    }
    else
    {
        return;
    }
}

堆排序

以线性时间建立二叉堆，然后依次通过下滤操作建立一个$max$堆，建立完成后依次通过deleteMax操作，将删除后的元素移至堆尾，完成操作。时间复杂度都为$O(nlogn)$。空间复杂度为$O(n)$。它是不稳定的排序算法。具体步骤如下：

  • 建立最大堆（build max heap）：若数组下标范围为0~n，考虑到单独一个元素是大根堆，则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始，向前依次构造大根堆，这样就能保证，构造到某个节点时，它的左右子树都已经是大根堆。* 堆排序（heapsort）：由于堆是用数组模拟的,在得到一个大根堆后，数组内部并不是有序的，因此需要将数组有序化。思想是移除根节点，并做下滤操作。第一次将heap[0]与heap[n-1]交换，再对heap[0…n-2]做下滤操作。第二次将heap[0]与heap[n-2]交换，再对heap[0…n-3]做下滤操作。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间，故操作完后整个数组就是有序的了。

示意图

duipaixu6.gif

C++实现

inline int leftChild(int i) {
        return 2 * i;
    }

    template &lt;typename Comparable&gt;
    void percDown(vector &lt;Comparable&gt; &amp; a, int i, int n) {
        int child;
        Comparable tmp;
        for(tmp=a[i]; leftChild(i)&lt;n; i=child) {        //leftChild确保在堆内计算 
            child = leftChild(i);
            if(child!=n-1 &amp;&amp; a[child]&lt;a[child+1]) {
                child++;
            }
            if(tmp &lt; a[child]) {
                a[i] = a[child];
            } else {
                break;
            }
        }
        a[i] = tmp;
    }

    template &lt;typename Comparable&gt;
    void heapSort(vector &lt;Comparable&gt; &amp; a) {
        for(int i=a.size()/2; i&gt;=0; i--) {        //建立max堆 
            percDown(a, i, a.size());
        }
        for(int j=a.size()-1; j&gt;0; j--) {        //进行堆排序
            swap(a[0], a[j]);
            percDown(a, 0, j);
        }
    }

版权属于：编码书生

本文链接：https://codess.cc/archives/55.html

所有原创文章采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可。
除特别注明，您可以自由的转载和修改，但请务必注明文章来源且不可用于商业目的。

最后修改：2018 年 11 月 16 日
© 允许规范转载
您的支持就是我持续更新的动力！